A formula is a concise way of expressing information symbolically or give a general relationship between quantities.

Formulas are used to solve equations with variables. For example the formula that describes the current flowing through a resistor when the voltage and resistance are known parameters is:

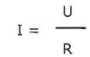
In which:

I representing the current in Ampere (A)

U the voltage in Volts (V)

R the resistance in Ohm (W)

In a general context a formula is applied to provide a mathematical solution fora real world problem. Formulae form the basis for all calculations.

Formulae are internationally standardized and enable professionals around the world to understand and use them appropriately.

Below is a selection of formulae, including those used in this book, with an explanation of their purpose. Also included are some short explanations of key parameters.

Some common electrical units used in formulas and equations are:

V = Volt, the unit of electrical potential.

W = Ohm, the unit of resistance.

A = Ampere, the unit of current

W = Watt, the unit of electrical energy or power.

VA = Volt Ampere, the product of volts and amperes.

Explanation: in direct current systems the volt ampere is the same as watts or the energy delivered. In alternating current systems the volts and amperes may not be 100% synchronous. When synchronous the volt amperes equals the watts on a wattmetre. When not synchronous volt amperes (VA) exceed watts (W)  cosⱷ = power factor, in short the ratio of watts to volt amperes or the ratio of the active (true or real) power to the apparent power.

Explanation: as this is an important issue in AC networks this is some explanation of the forms of power. There are three distinctive forms of power:

Active Power (P), measured in watts (W), is the power drawn by the electrical resistance of a network doing the actual work.

Apparent Power (S), measured in volt-amperes (VA), is the voltage on an AC network multiplied by all the current that flows in it. It is the vector sum of the active and the reactive power.

Reactive Power (Q), measured in volt-amperes reactive (VAR), is the power stored in and discharged by for instance inductive motors, transformers and solenoids. Reactive power is required for the magnetization of the steel cores but does not perform any action.

The power factor can be calculated from: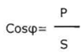 

In which P = active power (W)

S = apparent power (VA)

Low power factors should be avoided as the circuit's wiring has to carry more current than what would be necessary with a normal power factor of around 0,8 

The formula wheel below visualizes Ohm's law for the calculation of voltage (U), resistance (R), Power (P) and current (I).

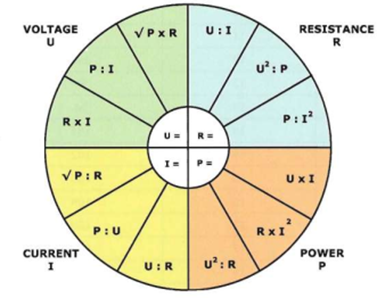
 Example: application Ohm's law

A 24V battery supplies power to a resistance of 48W The current can be calculated from:

I = U/R = 24/48 = 0,5A

The power can be calculated from: P = U2 : R = 242 : 48 = 12W

Multiples and Submultiples of Units

When large numbers are part of formulas and equations it is common practice to use prefix names of multiples and submultiples of units to ease reading of these. Some commonly used, also in this book, are: _ = micro, one-millionth or 0.000,001 m = milli, one-thousandth or 0.001 к = kilo, one thousand or 1,000 M = mega one million or 1,000.000

Examples: 1000 VA can also be written as lkVA, lOOOkVA can also be written as 1MVA which is: 1000 x 1000 = 1,000.000 VA. 

Energy and Power

Electrical energy      E = U x I x t

Active Power            P = U x I x  cosⱷ

Apparent Power       S = U x I

Reactive Power       Q = U x I x sinⱷ  

Current calculations generators and motors 

DC motors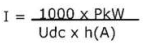   

Single-phase motor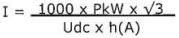   

Three phase motor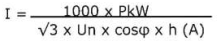   

Three phase generator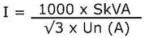   

Electrical Motor Efficiency

The electric motor efficiency can be calculated from: 

in which:            Winput

h = efficiency,

Php        = output horsepower (hp)

Winput = input electrical power (Watts)

For Winput one can substitute: U x I x V3 x cosⱷ